Intelligent design i aksjon: Optimalisering
Evolution News; 16. september 2015. Oversatt herfra.

Bilde 1: New York børsen, av Ryan Lawler (Eget arbeid) [Public domain], via Wikimedia Commons.

Tidligere har vi diskutert flere vitenskaper som er avhengige av prinsipper for intelligent design: blant dem arkeologi , rettsmedisin, kryptologi, informatikk SETI og SEETI , og mer. Nå gir en artikkel som beskriver en bemerkelsesverdig prestasjon muligheten til å utforske en annen: Optimalisering. Oppgaven fra University of Washingtons maskinlæringsforskere Abram Friesen og Pedro Domingos er godt beskrevet i en UW-nyhet -lenke . Jennifer Langston definerer optimalisering og forteller hvor nyttig feltet er.
-Nøkkelen til å løse mange av de viktigste problemene innen forretning, vitenskap og teknologi ligger i optimalisering – å finne verdiene for variabler som gir deg størst utbytte.
Enten det er hvilke aksjer du skal kjøpe, hvilke søkeresultater som skal returneres, hva som best forutsier utfallet av neste presidentvalg eller hvilke aminosyrer som skal settes sammen i et nytt medikament for å bekjempe malaria eller kreft, er optimalisering avgjørende for å få det vi ønsker. Når et problem er enkelt, kan vi programmere en datamaskin til å løse det. Når det er for komplekst til det, er optimalisering hvordan datamaskinen finner løsningen av seg selv.

Vi vet alle at en datamaskin ikke er i stand til å finne en løsning alene. En passende algoritme designet i den kan imidlertid tilsynelatende treffe jackpotten automatisk.
I hovedsak er optimalisering en søkestrategi. William Dembski behandler søk mye i sin siste bok, Being as Communion. Søk er nært knyttet til begrepet informasjon, som Dembski definerer som en vinnende prosess som realiserer muligheter ved å utelukke andre. Dersom den ønskede informasjonen er en løsning med størst nytte, må det søkes etter den informasjonen. Vitenskapen om optimalisering er derfor studiet av algoritmer eller strategier som realiserer den optimale løsningen ved å utelukke andre. Som sådan er det et informasjonsrikt felt.
Friesen og Domingos har oppnådd en imponerende prestasjon på dette feltet. Deres nye optimaliseringsalgoritme, kalt RDIS, utførte en optimaliseringsoppgave mellom 100 000 og 10 milliarder ganger mer nøyaktig i gjennomsnitt enn standardteknikker. Den var så bra at den vant hovedprisen på den 24. internasjonale felleskonferansen om kunstig intelligens i juli. Dette gigantiske spranget i optimalisering kan bidra til å øke hastigheten på å finne løsninger listet opp av Langston, og andre som veigjenkjenning for selvkjørende biler og å bestemme fold for tilpassede proteiner.

Domingos forklarer hvorfor optimalisering er viktigere enn mange er klar over:
"På noen måter er optimalisering det viktigste problemet du aldri har hørt om, fordi det dukker opp innen alle områder innen vitenskap, ingeniørvitenskap og næringsliv. Men mange optimeringsproblemer er ekstremt vanskelige å løse fordi de har et stort antall variabler som samhandler på intrikate måter, sier seniorforfatter Pedro Domingos, UW professor i informatikk og ingeniørfag.
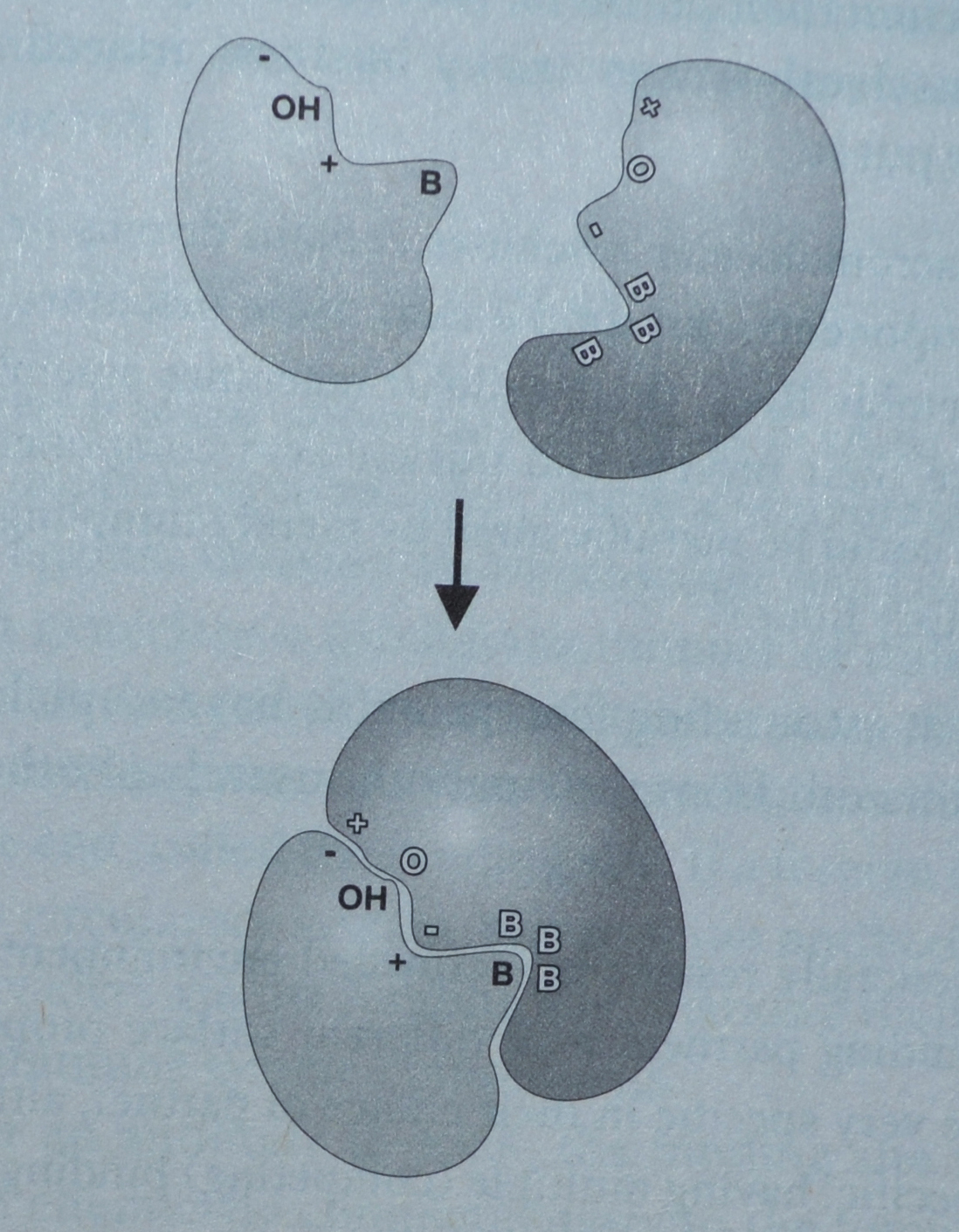
å finne ut proteinfolder har for eksempel vært et langvarig problem. Et protein begynner med en kjede av aminosyrer, men foldes til en kompleks, tredimensjonal form. For alle unntatt små proteiner har det å forutsi formen fra kjeden - gitt at aminosyrene samhandler på komplekse måter - trosset mange tidligere søk. RDIS kan være i stand til å fremskynde løsningen for syntetiske stoffer ved å optimalisere aminosyresekvensen for ønsket form. En annen applikasjon er å bestemme en tredimensjonal form fra en serie todimensjonale bilder.

Bilde 2. Proteiners passform -via form og ladning

å få RDIS til å fungere så bra var avhengig av flere teknikker. Den ene var en splitt-og-hersk-strategi kalt dekomponering. Ved å bryte ned problemet i mindre problemer og behandle dem som uavhengige problemer (selv om de ikke er det), konvergerte designerne mot den optimale løsningen mye raskere. En annen strategi er rekursjon. Disse og andre tekniske detaljer er beskrevet i artikkelen.
Optimalisering er ikke begrenset til AI eller datamaskiner. Hver logisk tenkende person står overfor optimaliseringsproblemer; f.eks. "Hvordan skal jeg fordele midlene mine for å optimalisere avkastningen på investeringen?" "Hvilke spillere skal jeg kalle opp for denne fotballskampen" Skal jeg sette av barna på skolen før jeg går til banken, eller etterpå?" "Hvor er trafikken sannsynligvis verst?" Optimalisering blir raskt vanskeligere ettersom kompleksiteten til problemet øker, angitt i en fyndig analogi:
-å løse optimaliseringsproblemer er som å bli stående med bind for øynene på toppen av en ås og bedt om å gå til havet. En måte å gjøre det på er å bedømme hvor du skal gå ved å føle deg rundt med foten og ta ett skritt av gangen i den bratteste nedadgående retningen. Det fungerer hvis det bare er én bakke. Men hvis du er på toppen av Himalaya, vil du raskt bli sittende fast fordi det er tusenvis av topper og daler og flate deler. Det er egentlig det som skjer med nåværende optimaliseringsalgoritmer.
"Hvis du er heldig, havner du kanskje i havet, men mer sannsynlig, havner du i en dal eller en innsjø," sa Domingos. "Hvis du kunne se hele landskapet, ville du sagt 'å, her må jeg gå', men problemet er at du ikke kan se overalt, og det kan heller ikke dagens algoritmer."

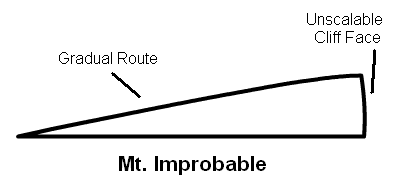Denne analogien vil høres kjent ut for de som er kjent med evolusjonsbiologi. "Egnethetslandskapet"-metaforen, lenke, laget av Sewall Wright omhandler også åser og daler; i den sammenheng representerer topper høy egnethet og daler representerer lav egnethet. Wright og påfølgende evolusjonsteoretikere innså at organismer kunne sette seg fast på lokale egnethets-topper (suboptima). å nå en høyere egnethets-topp vil kreve å mite egnethet midlertidig for å krysse en dal (se "Kompleksitet ved subtraksjon" -lenke). Og likevel ser det ofte ut til at dyr krysset daler, og mistet og gjenvant egenskaper flere ganger i henhold til fylogenetiske trær. Kan organismer nå høye nivåer av egnethet ved blinde, ikke-styrte prosesser?
Det er åpenbart at Friesen og Domingos ikke designet RDIS for å stole på blindt søk. Den ble intelligent utformet, på flere måter, hele veien. Først måtte de vite mye om eksisterende optimaliseringsverktøy. For det andre måtte de forstå målet sitt. For det tredje måtte de designe flere samvirkende faktorer for å nå målet sitt. Det er også et tilfelle av hierarkisk design. I en reell forstand måtte de optimalisere optimaliseringsverktøyet sitt.

Bilde 3. 'Blind klatring'

Intelligente designere vet hvordan de skal krysse daler for å nå høyere topper, fordi de kan se et fjernt mål og sikte mot det. Naturlig utvalg har intet framsyn. å fremstille neo-darwinismens mekanismer som optimaliseringsstrategier er derfor ønsketenkning (se "Evolutionary Computing: The Invisible Hand of Intelligence" -lenke). Dembski har vist i Being as Communion og i sin tidligere bok No Free Lunch at ingen søkestrategi er overlegen blindt søk - med mindre informasjon legges til systemet av intelligens.
Optimalisering er et godt eksempel på intelligent design i arbeid i vitenskapene. Ikke bare er feltet gjennomsyret av ID-konsepter fra start til slutt, det er også svært nyttig og bredt anvendelig. Så er ID en "vitenskapsstopper" som darwinister ofte hevder? Helt tvert i mot.